Embedding与向量数据库

Posted on

向量数据库

向量数据库(Vector Database),也叫矢量数据库，主要用来存储和处理向量数据。在数学中，向量是有大小和方向的量，可以使用带箭头的线段表示，箭头指向即为向量的方向，线段的长度表示向量的大小。两个向量的距离或者相似性可以通过欧式距离或者余弦距离得到。图像、文本和音视频这种非结构化数据都可以通过某种变换或者嵌入学习转化为向量数据存储到向量数据库中，从而实现对图像、文本和音视频的相似性搜索和检索。这意味着您可以使用向量数据库根据语义或上下文含义查找最相似或相关的数据，而不是使用基于精确匹配或预定义标准查询数据库的传统方法。向量数据库的主要特点是高效存储与检索。利用索引技术和向量检索算法能实现高维大数据下的快速响应。向量数据库也是一种数据库，除了要管理向量数据外，还是支持对传统结构化数据的管理。实际使用时，有很多场景会同时对向量字段和结构化字段进行过滤检索，这对向量数据库来说也是一种挑战

向量嵌入

对于传统数据库，搜索功能都是基于不同的索引方式(BTree、倒排索引等)加上精确匹配和排序算法(BM25、TF-DF)等实现的。本质还是基于文本的精确匹配，这种索引和搜索算法对于关键字的搜索功能非常合适，但对于语义搜索功能就非常弱。

例如，如果你搜索“小狗”，那么你只能得到带有“小狗”关键字相关的结果，而无法得到“柯基”“金毛”等结果，因为“小狗”和“金毛”是不同的词，传统数据库无法识别它们的语义关系，所以传统的应用需要人为的将“小狗”和“金毛”等词之间打上特征标签进行关联，这样才能实现语义搜索。而如何将生成和挑选特征这个过程，也被称为Feature Engineering(特征工程)，它是将原始数据转化成更好的表达问题本质的特征的过程。

但是如果你需要处理非结构化的数据，就会发现非结构化数据的特征数量会开始快速膨胀，例如我们处理的是图像、音频、视频等数据，这个过程就变得非常困难。例如，对于图像，可以标注颜色、形状、纹理、边缘、对象、场景等特征，但是这些特征太多了，而且很难人为的进行标注，所以我们需要一种自动化的方式来提取这些特征，而这可以通过Vector Embedding实现。

Vector Embedding是由AI模型（例如大型语言模型LLM)生成的，它会根据不同的算法生成高维度的向量数据，代表着数据的不同特征，这些特征代表了数据的不同维度。例如，对于文本，这些特征可能包括词汇、语法、语义、情感、情绪、主题、上下文等。对于音频，这些特征可能包括音调、节奏、音高、音色、音量、语音、音乐等。

例如对于目前来说，文本向量可以通过OpenAl的text-embedding-ada-O02模型生成，图像向量可以通过clip-vit-base-patch32模型生成，而音频向量可以通过wav2vec2-base-960h模型生成。这些向量都是通过AI模型生成的，所以它们都是具有语义信息的。

例如我们将这句话“Your text string goes here”用text-embedding-ada-002模型进行文本Embedding,它会生成一个1536维的向量，得到的结果是这样：“-0.006929283495992422，-0.005336422007530928,·,-454713225452536e-05,-0,024047505110502243”,它是一个长度为1536的数组。这个向量就包含了这句话的所有特征，这些特征包括词汇、语法，我们可以将它存入向量数据库中，以便我们后续进行语义搜索。

特征和向量

虽然向量数据库的核心在于相似性搜索(Similarity Search),但在深入了解相似性搜索前，我们需要先详细了解一下特征和向量的概念和原理。

我们先思考一个问题？为什么我们在生活中区分不同的物品和事物？

如果从理论角度出发，这是因为我门会通过源别不同事物之间不同的特征来识别种类，例如分别不同种类的小狗，就可以适过体型大小.毛发长层、旱子长短等烤证来区分。如下面这张照片按照体型序，可以看到体型拉入的狗靠近坐标抽右边，这样就能得到-一个体型特征的一维坐和对应的数值，从0到1的数字中得到每只狗在坐标系中的位置。

image.png

然而单靠一个体型大小的特征并不够，像照片中哈士奇、金毛和拉布拉多的体型就非常接近，我们无法区分。所以我们会继续观察其它的特征，例如毛发的长短。

image.png

这样每只狗对应一个二维坐标点，我们就能轻易的将哈士奇、金毛和拉布拉多区分开来，如果这时仍然无法很好的区分德牧和罗威纳犬。我们就可以继续再从其它的特征区分，比如鼻子的长短，这样就能得到个三维的坐标系和每只狗在三维坐标系中的位置。
在这种情况下，只要特征足够多，就能够将所有的狗区分开来，最后就能得到一个高维的坐标系，虽然我们想象不出高维坐标系长什么样，但是在数组中，我们只需要一直向数组中追加数字就可以了。
实际上，只要维度够多，我们就能够将所有的事物区分开来，世间万物都可以用一个多维坐标系来表示，它们都在一个高维的特征空间中对应着一个坐标点。
那这和相似性搜索(Similarity Search)有什么关系呢？你会发现在上面的二维坐标中，德牧和罗威纳犬的坐标就非常接近，这就意味着它们的特征也非常接近。我们都知道向量是具有大小和方向的数学结构，所以可以将这些特征用向量来表示，这样就能够通过计算向量之间的距离来判断它们的相似度，这就是相似性测量

相似性测量(Similarity Measurement)

上面我们讨论了向量数据库的不同搜索算法，但是还没有讨论如何衡量相似性。在相似性搜索中，需要计算两个向量之间的距离，然后根据距离来判断它们的相似度。而如何计算向量在高维空间的距离呢？有三种常见的向量相似度算法：欧几里德距离、余弦相似度和点积相似度。

欧几里得距离(Euclidean Distance)

欧几里得距离是用于衡量两个点（或向量）之间的直线距离的一种方法。它是最常用的距离度量之一，尤其在几何和向量空间中。可以将其理解为两点之间的“直线距离”。

其中，A和B分别表示两个向量，n表示向量的维度。

公式

对于两个向量A=(a1,a2,·,an)和B=(b1,b2,·,bn),它们之间的欧几里得距离可以计算为：

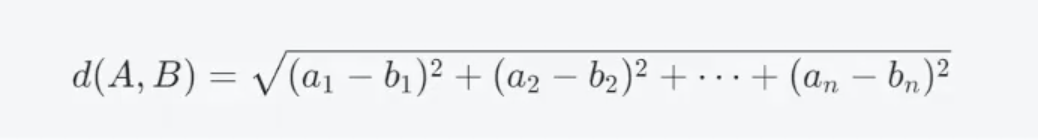
image.png

对应的图片为

image.png

image.png

欧几里得距离算法的优点是可以反映向量的绝对距离，适用于需要考虑向量长度的相似性计算。例如推荐系统中，需要根据用户的历史行为来推荐相似的商品，这时就需要考虑用户的历史行为的数量，而不仅仅是用户的历史行为的相似度。

余弦相似度(Cosine Similarity)

余弦相似度(Cosine Similarity)是一种用于衡量两个向量之间相似度的指标。它通过计算两个向量夹角
的余弦值来判断它们的相似程度。其值介于-1和1之间，通常用于文本分析和推荐系统等领域：

image.png

A·B是向量的点积
||A||和‖B||是向量的范数（即向量的长度）
计算步骤

  1. 点积计算：计算两个向量的点积，即各个对应元素相乘再求和。
  2. 范数计算：计算每个向量的范数，通常是欧几里得范数，即每个元素平方和的平方根。
  3. 代入公式：将点积和范数代入公式，得到余弦相似度。

image.png

特点

值域：结果在-1到1之间。1表示完全相似，0表示不相关，-1表示完全相反。
余弦相似度对向量的长度不敏感，只关注向量的方向，因此适用于高维向量的相似性计算。例如语义搜索和文档分类。

image.png

既然我们知道了可以通过比较向量之间的距离来判断它们的相似度，那么如何将它应用到真实的场景中呢？如果想要在一个海量的数据中找到和某个向量最相似的向量，我们需要对数据库中的每个向量进行一次比较计算，但这样的计算量是非常巨大的，所以我们需要一种高效的算法来解决这个问题。高效的搜索算法有很多，其主要思想是通过两种方式提高搜索效率：

1)减少向量大小一通过降维或减少表示向量值的长度。
2)缩小搜索范围一可以通过聚类或将向量组织成基于树形、图形结构来实现，并限制搜索范围仅在最接近的簇中进行，或者通过最相似的分支进行过滤。

我们首先来介绍一下大部分算法共有的核心概念，也就是聚类。

K-Means

我们可以在保存向量数据后，先对向量数据先进行聚类。例如下图在二维坐标系中，划定了4个聚类中心，然后将每个向量分配到最近的聚类中心，经过聚类算法不断调整聚类中心位置，这样就可以将向量数据分成4个簇。每次搜索时，只需要先判断搜索向量属于哪个簇，然后再在这一个簇中进行搜索，这样就从4个簇的搜索范围减少到了1个簇，大大减少了搜索的范围。

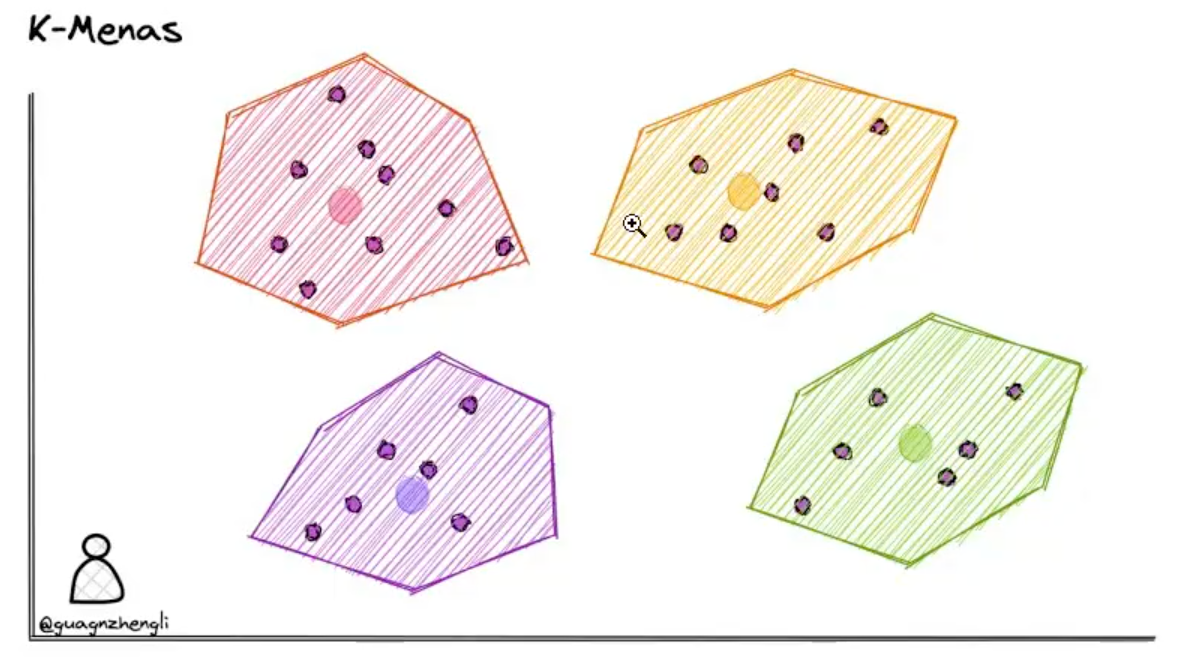
image.png

工作原理
1.初始化：选择k个随机点作为初始聚类中心。
2.分配：将每个向量分配给离它最近的聚类中心，形成k个簇。
3.更新：重新计算每个簇的聚类中心，即簇内所有向量的平均值。
4.迭代：重复“分配”和“更新”步骤，直到聚类中心不再变化或达到最大迭代次数。

举例说明
假设我们有一组二维向量（点），例如：「(1,2)，(2,1)，（4,5)，(5,4)，（8,9)川，我们希望将它们聚成四个簇（
k=4)。
1.初始化：随机选择四个点作为初始聚类中心，比如(1,2)、(2,1)、(4,5)和(8,9)。
2.分配：计算每个点到四个聚类中心的距离，将每个点分配给最近的聚类中心。
形成四个簇：[(1,2)]，[(2,1)]，[(4,5)，(5,4)]，[(8,9)]

  • 点(1,2)更接近(1,3)
  • 点(2,1)更接近(2,1)
  • 点（4,5)更接近（4,5)
  • 点(5,4)更接近（4,5)
  • 点(8,9)更接近(8,9)

3.更新：计算每个簇的新聚类中心

  • 第一个簇的聚类中心是(1,2)
  • 第二个簇的聚类中心是(2,1)
  • 第三个簇的新聚类中心是(4+5)/2，(5+4)/2)=(4.5,4.5)
  • 第四个簇的聚类中心是(8,9)

4.迭代：重复分配和更新步骤，直到聚类中心不再变化。

优点：通过将向量聚类，我们可以在进行相似性搜索时只需计算查询向量与每个聚类中心之间的距离，而不是与所有向量计算距离。这大大减少了计算量，提高了搜索效率。这种方法在处大规慎数据时尤其有效，可以显著加快搜索速度。

缺点，例如在搜索的时候，如果搜索的内容正好处于两个分类区域的中间，就很有可能遗漏掉最相似的向量。

Hierarchical Navigable Small Worlds (HNSW)

除了聚类以外，也可以通过构建树或者构建图的方式来实现近似最近邻搜索。这种方法的基本思想是每次将向量加到数据库中的时候，就先找到点它最相邻的向量，然后将它们连接起来，这样就构成了一个图。当需要搜索的时候，就可以从图中的某个节点开始，不断的进行最相邻捷豪和最短路径计算，直到找到最相似的向量。这种算法能保证搜索的质量，但是如果图中所以的节点都以最短的路径相连，如图中最下面的一层，那么在搜索的时候，就同样需要遍历所有的节点。

image.png

解决这个问题的思路与常见的跳表算法相以，如下图要搜索跳表，从最高层开始，沿着具有最长“跳过的边向右移动。如果发现当前节点的值大于要搜索的值-我们知道已经超过了目标，因此我们会在下一级中向前一个节点。

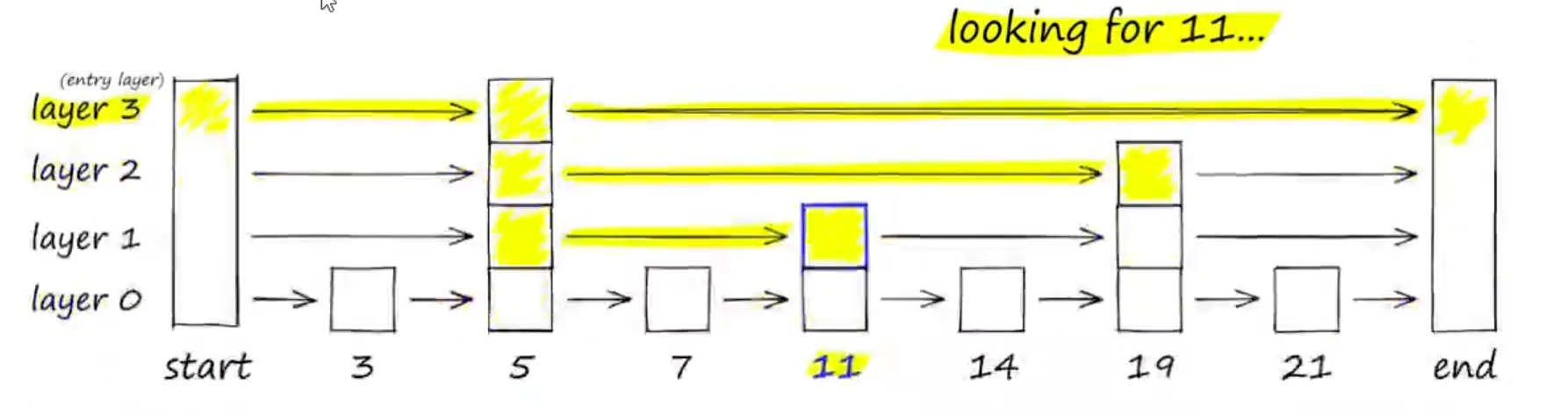
image.png

通过一个简单的例子来说明HNSW的工作原理。
假设我们有以下五个二维向量：

  • A=(1,2)
  • B=(2,3)
  • C=(3,4)
  • D=(8,9
  • E=(9,10)
    我们要使用HNSW来找到与查询向量Q=(2,2)最相似的向量。

image.png

image.png

总结: 通过这种层次化的搜索过程，HNSW能够快速缩小搜索范围，在大规模数据中高效找到近以最近邻。

基于Embedding的问答助手和意图匹配

Embedding models(嵌入模型)

Embeddings类是一个专为与文本嵌入模型进行交互而设计的类。有许多嵌入模型提供商（如OpenAl.Cohere、Hugging Face等)-这个类旨在为它们提供一个标准接口。

Embeddings类会为文本创建一个向量表示。这很有用，因为这意味着我们可以在向量空间中思考文本，并做一些类似语义搜索的事情，比如在向量空间中寻找最相似的文本片段。

LangChain中的基本Embeddings类提供了两种方法：一个用于嵌入文档，另一个用于嵌入查询。前者，embed_documents接受多个文本作为输入，而后者.embed_query接受单个文本。之所以将它们作为两个单独的方法，是因为一些嵌入提供商对文档（要搜索的文档）和查询（搜索查询本身）有不同的嵌入方法。

.embed_.query将返回一个浮点数列表，而.embed._documents将返回一个浮点数列表的列表。

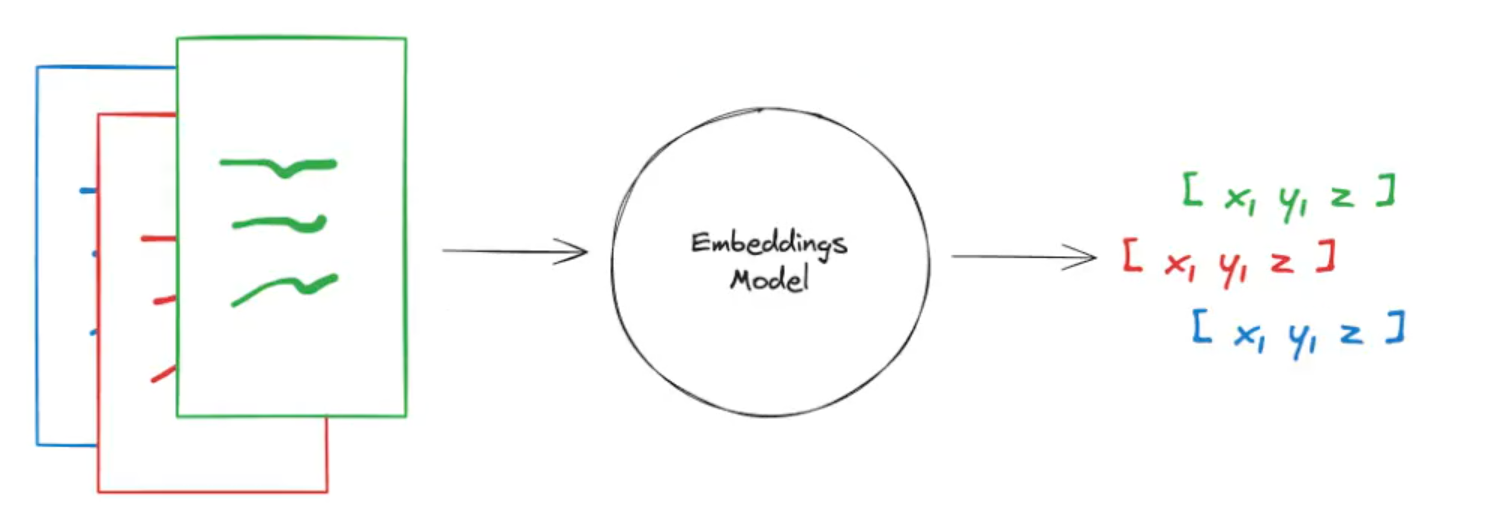
image.png

设置OpenAl
首先，我们需要安装OpenAl合作伙伴包：

1
pip install langchain-openai

访问AP需要一个API密钥，您可以通过创建帐户并转到这里来获取它。一旦我们有了密钥，我们希望通过运行以下命令将其设置为环境变量：

1
export OPENAI_API KEY="..."

如果您不想设置环境变量，可以在初始化OpenAl LLM类时通过api_key命名参数直接传递密钥：

1
2
from langchain_openai import OpenAIEmbeddings
embeddings_model OpenAIEmbeddings(api_key="...")

否则，您可以不带任何参数初始化：

1
2
from langchain_openai import OpenAIEmbeddings
embeddings_model OpenAIEmbeddings()

完整的Case

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

# pip install langchain-openai

from langchain_openai import OpenAIEmbeddings
embeddings_model = OpenAIEmbeddings()
embeddings = embeddings_model.embed_documents(
	[
		"嗨！",
		"哦，你好！",
		"你叫什么名字？",
		"我的朋及们叫我World",
		"Hello World！"
	]
)
#第一个打印是embeddings/的文本数量，第二个打印是第一段文本的embed中ing向量维度
print(len(embeddings),len(embeddings[0]))

image.png

嵌入单个查询(embed query)

使用.embed_query来嵌入单个文本片段（例如，用于与其他嵌入的文本片段进行t比较）。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
# pip install langchain-openai

from langchain_openai import OpenAIEmbeddings
embeddings_model = OpenAIEmbeddings()
embeddings = embeddings_model.embed_documents(
	[
		"嗨！",
		"哦，你好！",
		"你叫什么名字？",
		"我的朋及们叫我World",
		"Hello World！"
	]
)
embedded_query=embeddings_model.embed_query("对话中提到的名字是什么？")
#查询嵌入的前五个值
print(embedded_query[:5])

输出结果

1
2

[0.603292866277936101,-0.689463472291827282,0.03418809175491333,-0.8811715596774592996,...]

问答助手

从知识库中，找到一个和问题最接近的类似问题。我的知识库集合为：

1
2
3
4
"OpenAI的ChatGPT,是一个强大的语言模型。",
"天空是蓝色的,阳光灿烂。",
"人工智能正在改变世界。",
"Python是一种流行的编程语言。"

完整Case

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47

from openai import OpenAI
#pip install numpy
from numpy import dot
from numpy.linalg import norm
client = OpenAI()

#定义调用Embedding API的函数
def get_embedding(text):
    response = client.embeddings.create(
        input=text,
        model="text-embedding-ada-002"
    )
    return response.data[0].embedding

def cosine_similarity(vec1,vec2):
#计算并返回两个向量之间的余弦相似度，公式为：两个向量的点积除以它们范数的乘积。
    return dot(vec1 , vec2) / (norm(vec1) * norm(vec2))

# 定义一个函数search_documents,该函数接受一个查询字符串query和一个文档列表documents作为输入。
def search_documents(query,documents):
    #调用get_embedding函数生成查询字符串的嵌入向量query_embedding。
    query_embedding = get_embedding(query)
    #对每个文档调用get_embedding函数生成文档的嵌入向量，存储在document_embeddings列表中。
    document_embeddings = [get_embedding(doc) for doc in documents]
    #计算查询嵌入向量与每个文档嵌入向量之间的余弦相似度，存储在similarities列表中
    similarities = [cosine_similarity(query_embedding,doc_embedding) for doc_embedding in document_embeddings]
    #找到相似度最高的文档的索引most_similar_index。
    most_similar_index = similarities.index(max(similarities))
    #返回相似度最高的文档和相似度得分。
    return documents[most_similar_index],max(similarities)


#测试文本搜索功能
if __name__=="__main__":
    documents = [
        "OpenAI的ChatGPT,是一个强大的语言模型。",
        "天空是蓝色的,阳光灿烂。",
        "人工智能正在改变世界。",
        "Python是一种流行的编程语言。"
    ]
    query="天空是什么颜色的？"

    most_similar_document,similarity_score = search_documents(query,documents)

    print(f"最相似的文档：{most_similar_document}")
    print(f"相似性得分：{similarity_score}")